Have you wondered what the expected reward for your Peercoin is?
Do you know what the best size for your outputs is?
I’m pleased to share a Python Jupyter notebook that shows the expected annual reward for different output sizes. This work was produced by me in discussion with @Nagalim who has provided many ideas and insights. This notebook is able to produce charts like this:
The numbers are average theoretical expectations for the given parameters and assume continuous minting without consideration of stale blocks. Actual results may vary.
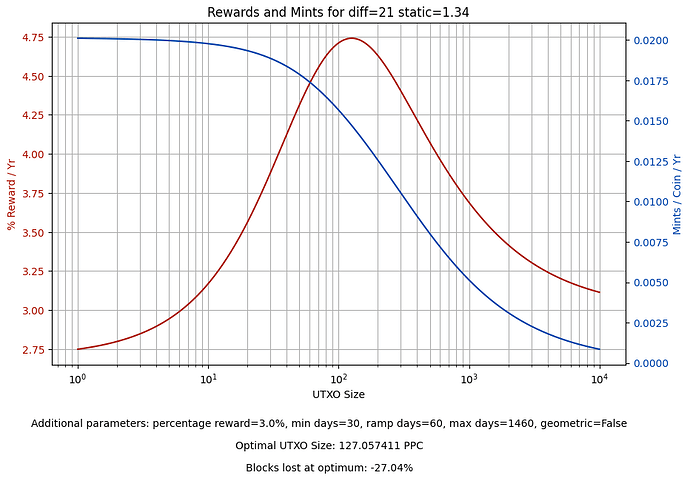
This shows the expected percentage reward and number of mints per coin over a year, for different output sizes, according to the given difficulty and static reward. Currently it produces 127.057411 PPC as the optimal size for a reward of 4.74%.
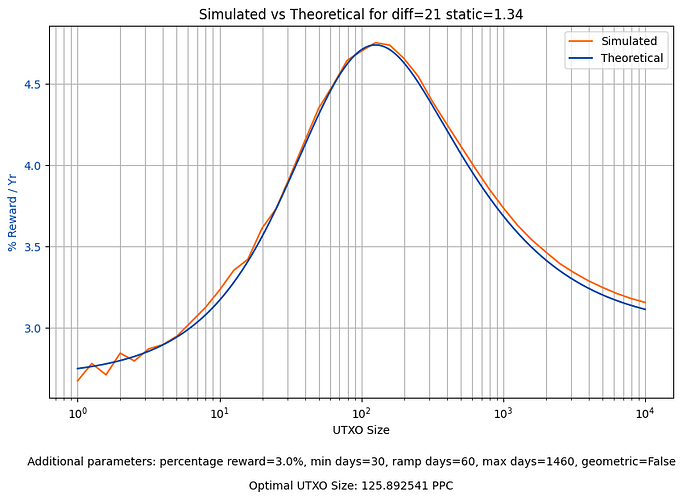
The notebook also simulates a hypothetical wallet to compare with the theoretical rewards. The simulation comes reasonably close:
The software is available open-source here: GitHub - MatthewLM/OptimumPeercoinUTXO: Find the optimal UTXO size for Peercoin minting
Optimisation of output size
It is possible to manually split and combine outputs to the theoretical optimum, but it would be better for this to be automatically done by the client. The current split function will split an output in half when minting within 90 days. This doesn’t take into consideration the optimum value and may take several iterations to optimise a large output due splitting only halving at most.
Theoretical rewards are easy to calculate. The client can search for the peak value. Once the optimum output size is determined, the output can be split to be as close to the optimum as possible.
The client may take into account non-continuous minting by adjusting the target size upward with a certain tolerance for lost reward assuming continuous minting (eg. increase target size up-to a 10bps loss in reward). This may not be needed as it is desirable to incentivise continuous minting in any case.
To determine how many times an output should be split, the resulting output sizes should be as close to the optimum as possible on a log-scale. The maximum split should be limited to avoid exceeding the 1KB fee-free limit of the coinstake transaction. The limit can be determined by calculating the size of the coinstake and restricting it to 1KB. Without going into details (see WolframAlpha for that), the solution for this is:
min(floor(0.5*((4*((outputSize/optimumSize)^2)+1)^0.5 + 1)), maxOutputSplit)
Inputting the current output size and target optimum size will yield the number of splits, limited by maxOutputSplit.
Optimising outputs should increase the mint-rate and rewards for a wallet and improve security through raising difficulty with all else being equal.
Future considerations
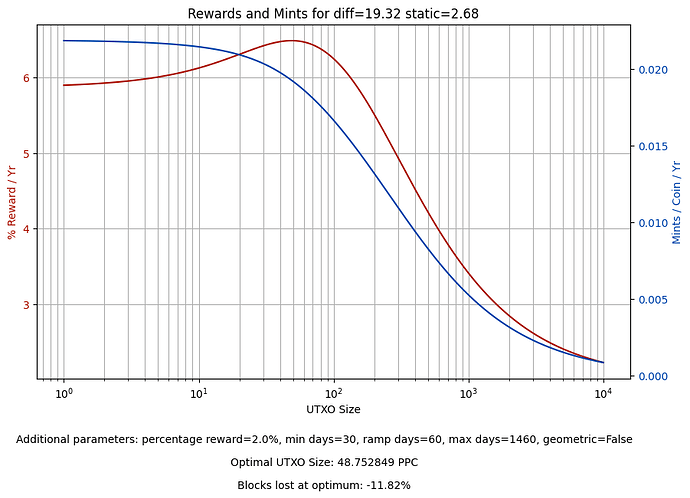
Since small outputs also see a drop-off in reward, those outputs could be recombined. However, it may be more appropriate to wait for a hard-fork change in the network parameters to benefit smaller outputs. The notebook allows playing around with those parameters to see different effects, though the effect of any changes on minter involvement is difficult to predict. Here is one example of changing the coinage reward to 2% and static reward to 0.5% which causes the low-value outputs to have less reward drop-off:
Note that this change also reduces the drop in mint-rate for the optimum output size to only -11.82%.
Changes can also be considered to:
- Incentivise continuous minting or minting in general.
- Simplify minting mechanics.
- Reduce the block interval and therefore confirmation times.
- Reduce loss in block-rate at the economic optimum.
- Decrease initial wait to start minting blocks.
These changes should be considered separately to output split optimisation which can be developed without needing a hard-fork.